拉格朗日乘数法

拉格朗日乘数法的推导

  求函数极值是微积分研究的重要问题。拉格朗日乘数法解决的核心问题就是对于自变量拥有约束条件（尤其是约束条件不能被化为显函数）的多元函数，如何求出其极值。以二元函数为例，对于函数$z=f(x,y)$,有约束条件$g(x,y)=c$.假设$z$在$(x_0,y_0)$处取得极值，并且$f(x,y),g(x,y)$在$(x_0,y_0)$的领域内都具有连续的一阶偏导数.

  那么，首先借助几何直观来观察取得极值的必要条件.

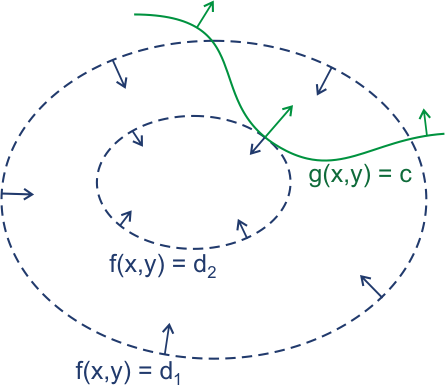
如上图所示，作出$z=f(x,y)$的等高线图。此时不难发现：
约束曲线$g(x,y)=c$在与$z=f(x,y)$的某条等高线$f(x,y)=d_2$相切时,$z$取得极值。此点处$f(x,y)=d_2$和$g(x,y)=c$拥有共线的法向量，因此二者的梯度也共线$\Rightarrow \mathbf{grad}{f(x_0,y_0)}=-\lambda\mathbf{grad}(g(x_0,y_0)-c)\Rightarrow f_x\boldsymbol{i}+f_y\boldsymbol{j}=-\lambda(g_x\boldsymbol{i}+g_y\boldsymbol{j})$

$$\Rightarrow \begin{cases} f_x(x_0,y_0)+\lambda g_x(x_0,y_0)=0\\ f_y(x_0,y_0)+\lambda g_y(x_0,y_0)=0\\ g(x_0,y_0)-c=0 \end{cases}$$

这就得到了函数$z=f(x,y)$,在约束条件$g(x,y)=c$取得极值的必要条件.

通过几何直观了解了拉格朗日乘数法的意义，下面尝试通过微积分的方法进行严格的证明.

  由前提条件,由隐函数存在定理得,$g(x,y)=c$确定了一个连续且导函数连续的函数$y=h(x)$,
将此函数带入$f$,得到$z=f(x,h(x))$.则$f(x,y)$在$(x_0,y_0)$取得极值等价于$f(x,h(x))$在$x=x_0$处取得极值.

由单变量微积分的知识得,取得极值时$\displaystyle{\frac{d z}{d x}|_{x=x_0}=f_x(x_0,y_0)}+f_y(x_0,y_0)\frac{d y}{d x}|_{x=x_0}=0$,而由隐函数求导可以得
${
\displaystyle\frac{d y}{d x}|_{x=x_0}=-\frac{g_x(x_0,y_0)}{g_y(x_0,y_0)}.
}$

  代回前式可以得到$\displaystyle{f_x(x_0,y_0)-\frac{g_x(x_0,y_0)}{g_y(x_0,y_0)}f_y(x_0,y_0)=0\Rightarrow \frac{f_x}{g_x}=\frac{f_y}{g_y}}$.这与由几何直观推出的梯度成比例一致.记比值为$\lambda$,则约束条件下取得极值的必要条件为

$$f_x(x_0,y_0)+\lambda g_x(x_0,y_0)=0$$ $$f_y(x_0,y_0)+\lambda g_y(x_0,y_0)=0$$ $$g(x_0,y_0)-c=0$$

  构造辅助函数函数$L(x,y,\lambda)=f(x,y)+\lambda g(x,y)$.将$L(x,y,\lambda)$记为拉格朗日(Lagrange)函数，记$\lambda$为拉格朗日算子，则取得极值的必要条件记为

$$L_x(x_0,y_0,\lambda_0)=0$$ $$L_y(x_0,y_0,\lambda_0)=0$$ $$g(x_0,y_0)-c=0$$

这就是拉格朗日乘数法

  拉格朗日乘数法可以推广到高维,同时拉格朗日算子可以有多个。如对于$u=f(x,y,z)$存在约束条件$\varphi(x,y,z)=0,\psi(x,y,z)=0$,
则拉格朗日函数写为$L(x,y,z,\lambda,\mu)=f(x,y,z)+\lambda\varphi(x,y,z)+\mu\psi(x,y,z)$,取得极值的必要条件为

$$L_x(x,y,z,\lambda,\mu)=0$$ $$L_y(x,y,z,\lambda,\mu)=0$$ $$L_z(x,y,z,\lambda,\mu)=0$$ $$\varphi(x,y,z)=0$$ $$\psi (x,y,z)=0$$

解决方法使用的思路

  无论是几何直观还是严格推导，得出拉格朗日乘数法都利用了约束条件的自由度比原函数少的特征.

  在几何直观中,由于约束条件的几何图形维数始终比原函数的几何图形少1(在三维下分别是曲线和曲面),因此在约束条件下取得极值时,约束函数一定与原函数的”等高线”相切,由此推出了切线/切面平行,并根据梯度平行得到了必要条件.

  在严格推导中,由隐函数存在定理,利用对约束条件得到自变量之间的函数关系,最终将原函数由多元函数变为一元函数,利用单变量微积分的方法得出了必要条件.

拉格朗日乘数法的应用

  拉格朗日乘数法的应用十分广泛，任何多元函数在相等的约束条件下求极值都可以使用。

典型的应用:求离散分布的最大熵问题可以应用在机器学习中的最大熵模型中:

对离散分布$
{
f(p_1,p_2,\cdots,p_n)=-\sum_{k=1}^np_k\log_2p_k
}$求最大熵.

由于所有概率的和为1,因此约束条件为$
{
g(p_1,p_2,\cdots,p_n)=\sum_{k=1}^np_k=1
}$

可以使用拉格朗日乘数法找到最高熵.对于所有$k$从1到$n$，${
\displaystyle\frac{\partial}{\partial p_k}(f+\lambda(g-1))=0
}$

${
\Rightarrow -(\frac{1}{\ln 2}+\log_2p_k)+\lambda=0\Rightarrow p_k
}$全部相等,得到${
p_k=\frac{1}{n}
}$,因此均匀分布时可以得到最大熵的值.

  此外，还有经济学中的约束最优化等问题，都广泛应用了拉格朗日乘数法.